I then introduced a third sphere, and to my astonishment, the situation changed completely. Like I said, any geometric figure turns into numbers in the depths of my mind. The sphereless, one-sphere, and two-sphere universes all showed up as a single equation or a few equations, like a few lonesome leaves in late fall. But this third sphere gave “emptiness” life. The three spheres, given initial movements, went through complex, seemingly never-repeating movements. The descriptive equations rained down in a thunderstorm without end.

(Taken from The Three-Body Problem by Cixin Liu)

Introduction

The Three-Body Problem was theorized by Issac Newton in order to determine the long term stability of the Earth-Moon-Sun system. No general closed form solution exists for the problem, resulting in a system that is chaotic for most initial conditions. Modeling the system is useful in astrophysics to model the long term trajectories of stellar systems; trajectories of bodies in a three-body system are impossible to determine without knowing its initial conditions to infinite precision. This report aims to highlight the various numerical and analytical methods used to solve the problem and comment on their practicality.

Classical Mechanics

Newton’s Propositions

In Philosophæ Naturalis Principia Mathematica, Issac Newton qualitatively comments on the motion of a third body under the influence of the gravity of two interacting bodies, using the Sun, the Earth and the Moon as an example. He described a set of three differential equations to determine their acceleration. The proposition then describes the complexity of motion of three similar masses moving under the influence of gravity.

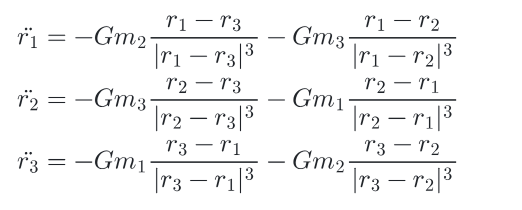
Note: Mathjax renderer has a personal vendetta against me, which is why the above equations are in a screenshot rather than in text.

Restricted Three Body Problem

Under certain conditions, a system of three gravitationally interacting bodies is a largely non-chaotic system. In a “restricted” three-body problem, a small mass moves under the influence of large masses. Since the mass is negligible, its influence on the larger bodies can be neglected during calculations. For example, in the Alpha Centauri star system, Proxima Centauri orbits two larger stars (Alpha Centauri A and B).

Analytical Solutions

Lagrange’s Family of Solutions

In 1772, Lagrange determined a family of solutions in which three masses are at an equilateral triangle at all times. Jupiter and the Greek and Trojan family of asteroids, for example, form an equilateral triangle and interact like a three-body system. Lagrange determined a family of five solutions - points that are viewed from reference frames that rotate with the masses - which are known as Lagrangian points. However, his family of solutions only apply to a circular restricted three-body problem which require very specific conditions in order to work, which is why Lagrange’s method cannot be used as a general solution to the problem.

Karl Sundman’s Approximation

In 1912, Karl Sundman proved the existence of an analytical solution to the three-body problem that corresponds to values of time $t^{1/3}$. His solution is a power series that was discovered while searching for singularities; in Sundman’s three-body problem, this occurred when the angular momentum of the system vanishes, i.e., points at which binary or triple collisions occur. The set of nine differential equations that govern the three-body problem, which has 18 degrees of freedom, is restricted to 12 degrees of freedom by using the center of mass of two of the bodies as a frame of reference. Sundman’s approximation converges for all real values of t, however the series converges far too slowly for practical purposes; astronomers estimate that if Sundman’s calculations were used in astronomical observations, computations would involve $10^{8000000}$ terms.

What Now?

Over the years, mathematicians proved that no general solution to the three-body problem can be found analytically. For a restricted three-body system, Henri Poincaré concluded that an infinite number of periodic solutions exist, but without knowing the initial conditions of a system to infinite precision, it is impossible to study its long-term behavior.

Using THREE.JS To Simulate Three-Body Interactions

A few months ago, I wrote code using Pygame and Python to simulate a 2D version of the three body problem. To more realistically simulate it, I decided to use JavaScript and a 3D environment using Three.JS.

Clarification: Even though a system is chaotic, it is still possible to simulate it. The bodies in three-body follow a set of equations that update their positions at fixed intervals. The simulation’s scope is limited to the influence of those three bodies alone, and while the long term behavior of each simulated interaction can be predicted, this is possible only because the initial conditions of the simulation are known.

How It’s Done

Three.js is an opensource JavaScript library that can create and display 3D computer graphics in the browser using WebGL.

The equation for the force between two masses (m1 and m2) due to gravity is given by:

$F = G × \frac{m_{1}m_{2}}{R^{2}}$

Knowing the masses of the object, we can calculate the acceleration of the object.

$F = m × a$

We can then calculate the velocity of the object.

$v = u + a × t$

t is a small interval of time and u is the previous value of velocity.

First I defined a Star class that contains all the information for each body. The distances are scaled in the ratio $1:10^{6}$ meters.

The values of force, velocity, acceleration, and position are stored as 1x3 matrices (3 dimensional vectors). The Star class also contains methods to update the position according to the value of the body’s acceleration.

I then defined a class for the gravity Engine. Its primary function is to calculate the force vectors for each body in the engine. Technically, this engine can be used to simulate any number of gravitationally interacting bodies, but for the purpose of this project, I’m limiting the number of bodies to 3.

Finally, the engine updates at every frame using Three.js’s animation function.

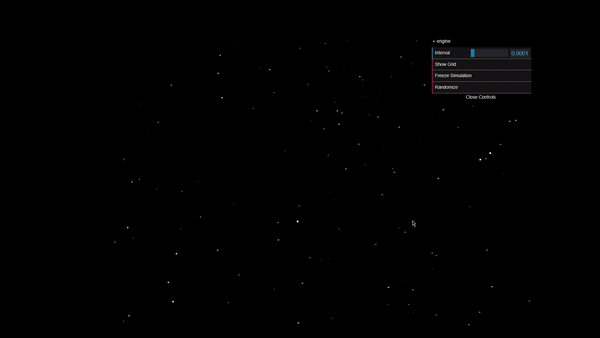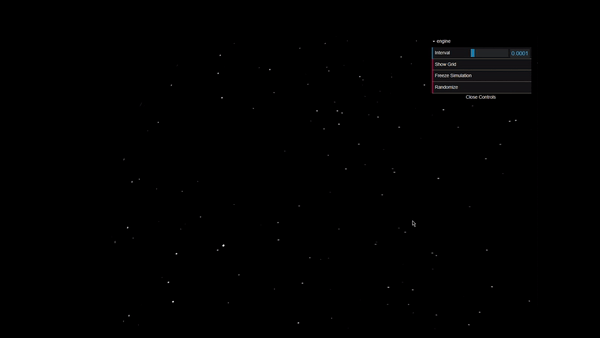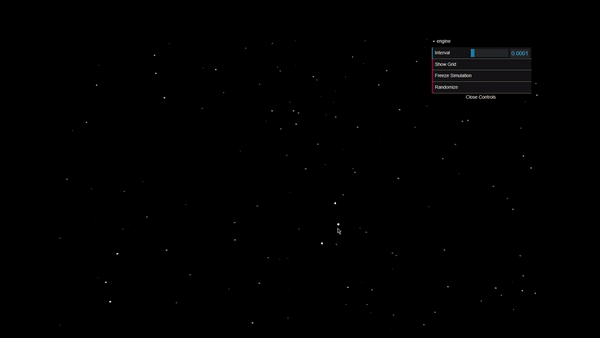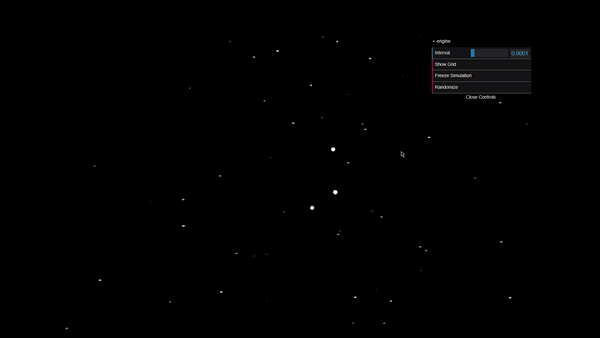
A live demo of the project is available here.

There’s features to pan & zoom around the area.

The top right corner has a set of controls for the simulation. Through it, you can change the intervals at which the force is calculated.

Finally, I’ve added boundary conditions. If a body exits a radius of $8 X 10^{8}$ meters, the force is so negligible that the simulation is no longer a system of three bodies, which is why the simulation automatically resets.

Conclusion

I had a lot of fun collecting information for this project. This article along with the simulation is a part of a larger upcoming project that talks about chaos theory and determinism.

I ended up collecting so much information because of a course on Non-Linear Dynamics at my university. I’ve attached the little homework assignment that inspired this project to this article.

References:

• Three Body Problem with Python
• On Periodic Solutions of the three-body problem
• Newton’s Philosophae Naturalis Principia Mathematica
• A (Less than practical) Solution to the N-Body Problem
• Exposition of Sundman’s Regularization of The Three Body Problem
• Github Repository to my simulation
• Almaric’s Gravity Engine

While I’m at it, here’s a few other links.

• My Youtube Channel
• Instagram