Python Playground Chapter 3: Conway's Game of Life!
In October 2022, I started reading Python Playground and wrote an article to mark the day I started.
As of today, I finished reading and coding for the third chapter of Python Playground. This chapter may be my favorite one yet as it involved creating a simulation: specifically a simluation of life using simple rules.
Rules of the Game
The Game of Life, designed by John Conway, is built on a grid of nine squares or cells. Each cell can carry one of two values: ON or OFF. The rules for the simulation are as follows:
- If a cell that is ON has fewer than two neighbors that are ON, it turns OFF (representing underpopulation).
- If a cell that is ON has either two or three neighbors that are ON, the cell remains ON (representing a stable population).
- If a cell is ON and has more than three neighbors that are ON, it turns off (representing overpopulation).
- If a cell is OFF and has three neighbors that are ON, it turns ON (representing population growth).
Sets of 9-celled grids form a larger grid which acts as the ground for the simulation to take place. However, at the corners of the grid, the rules of the game become hard to implement as the cells along the edges have less than eight neighbors.
To counter the issue, the grid is treated as a torus - a shape with no edge. Imagine folding a piece of paper to join two of its edges to form a cylinder and then twisting the two ends of the cylinder to meet.
These grid conditions operate similar to Pacman’s boundaries where going to the edge of the screen puts you on the opposite edge of the screen.
In code, it’s implemented on a 2D array grid of size N*N.
right = grid[i][(j+1)%N]
right would represent the cell directly to the right of the selected cell (grid[i][j]).
To find the number of ON cells around a cell, we find the total value of all nine cells.
total = int((grid[i, (j-1)%N] + grid[i, (j+1)%N] +
grid[(i-1)%N, j] + grid[(i+1)%N, j] +
grid[(i-1)%N, (j-1)%N] + grid[(i-1)%N, (j+1)%N] +
grid[(i+1)%N, (j-1)%N] + grid[(i+1)%N, (j+1)%N])/255)
# the final sum is divided by 255 as 255 in each cell represents 'ON'
Simulation
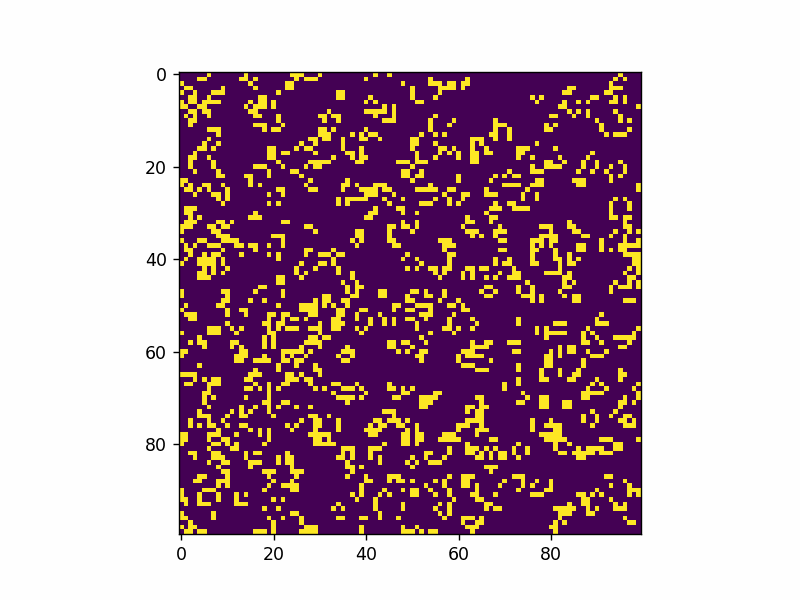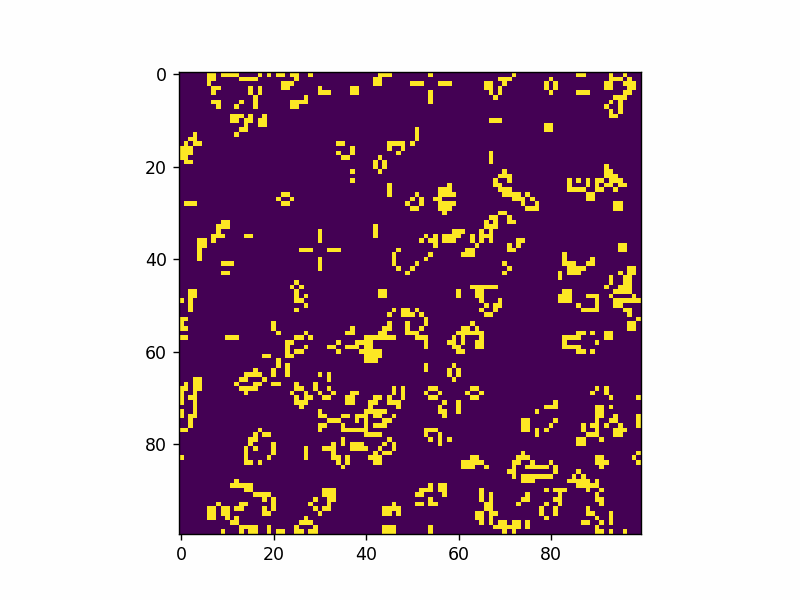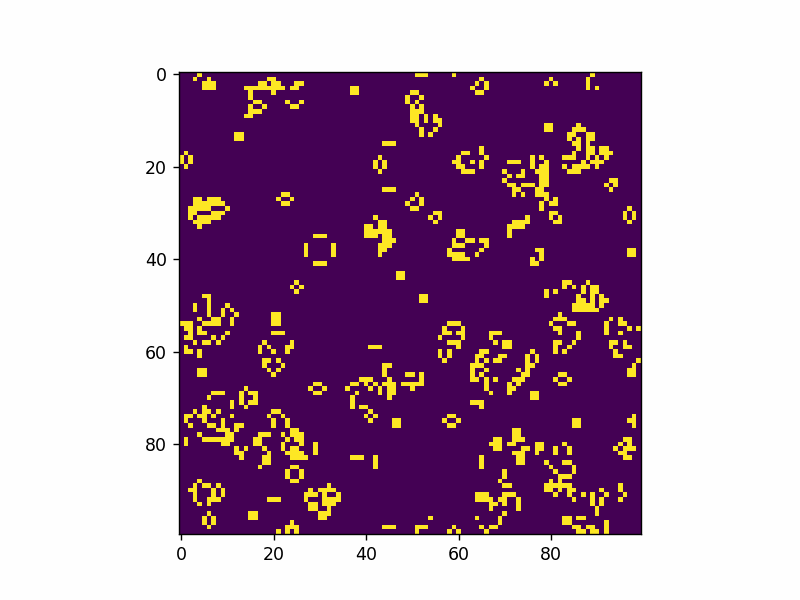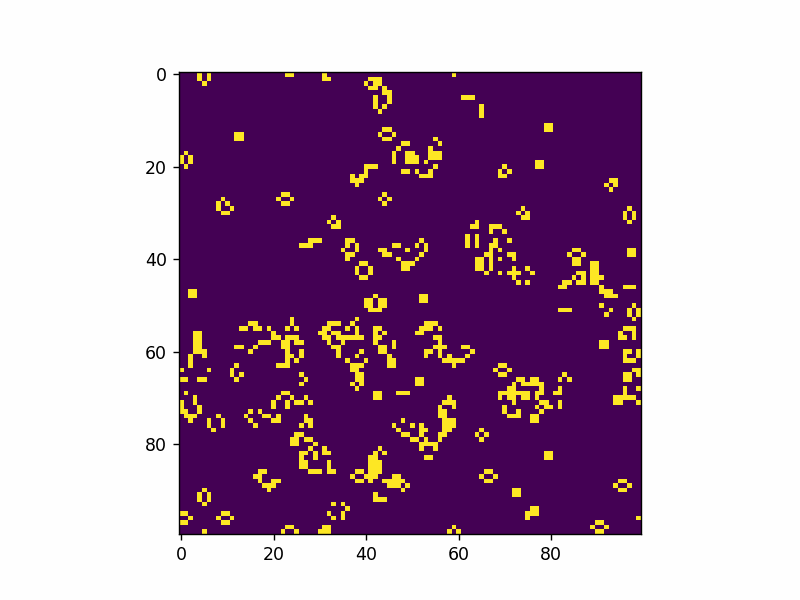
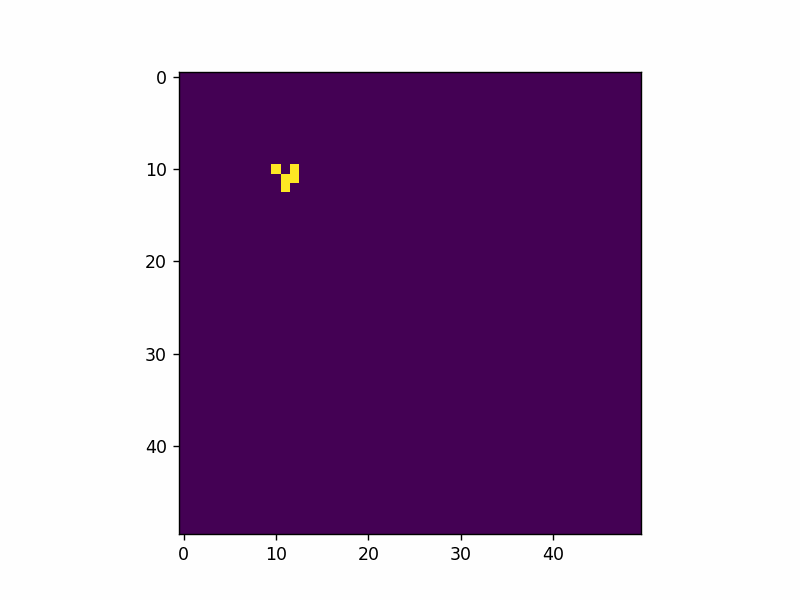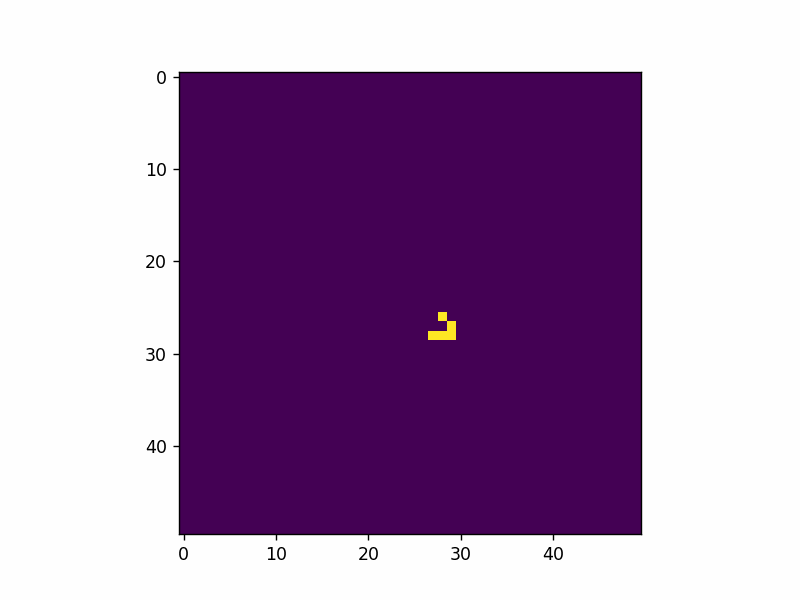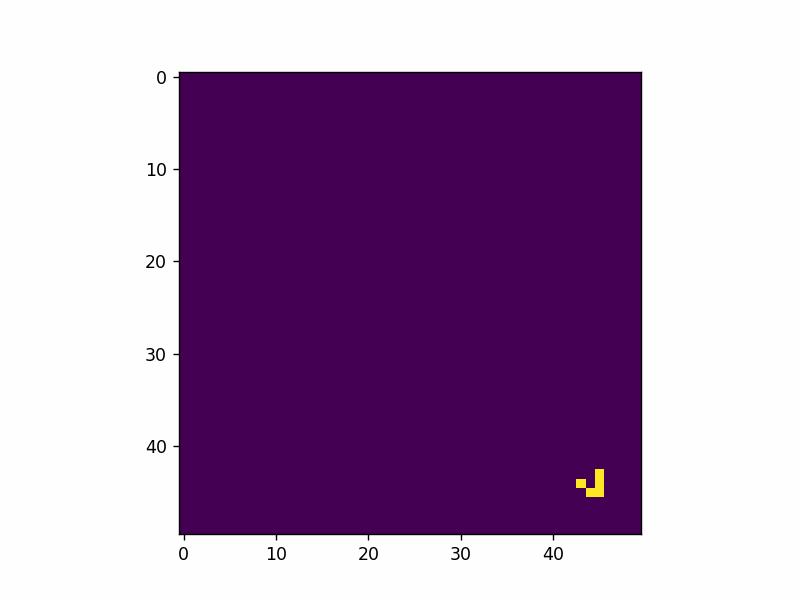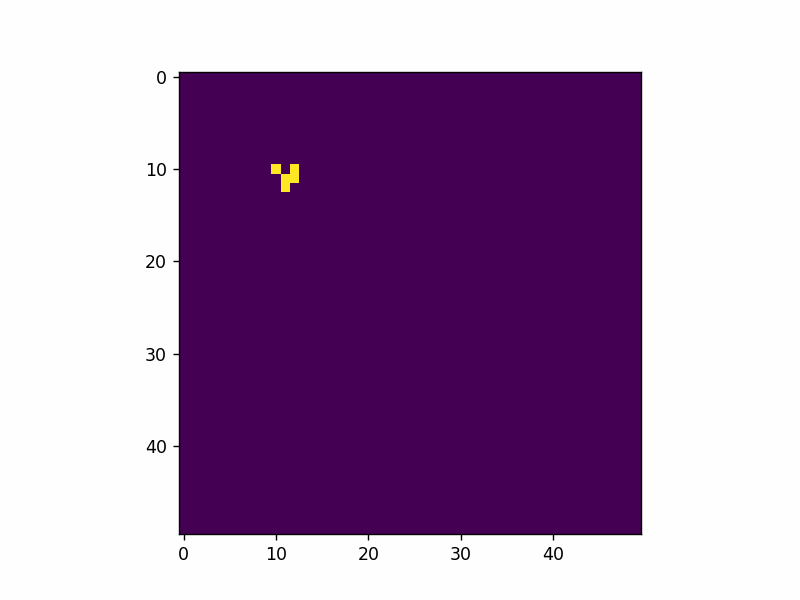
Here’s an example of adding a single glider pattern into the simulation.
Here’s an example of using a “gosper gun”.
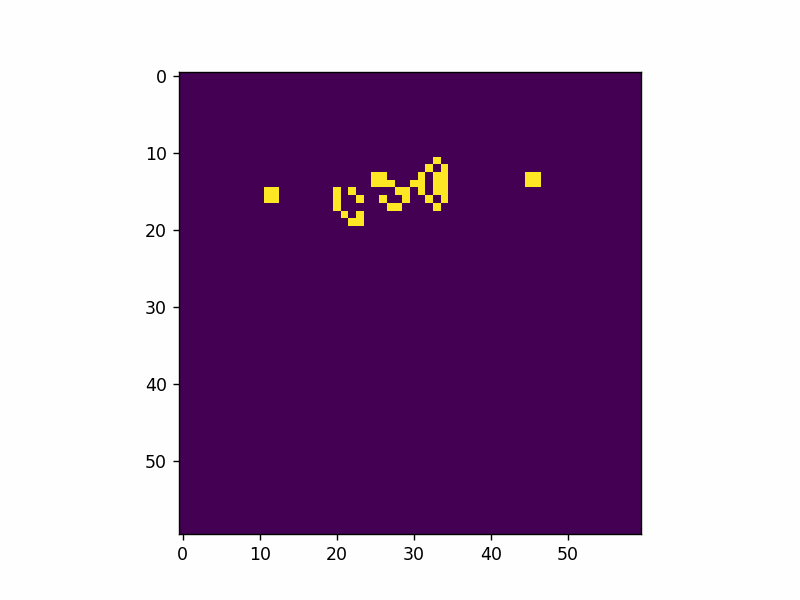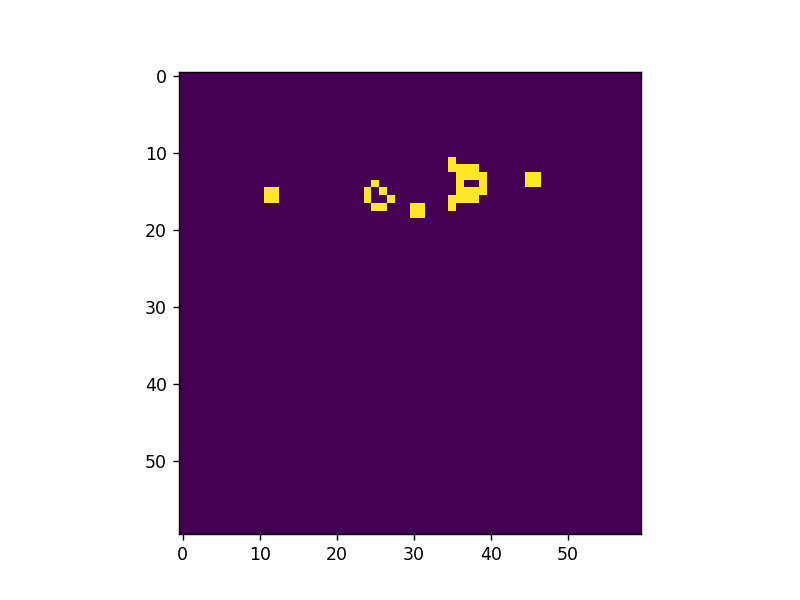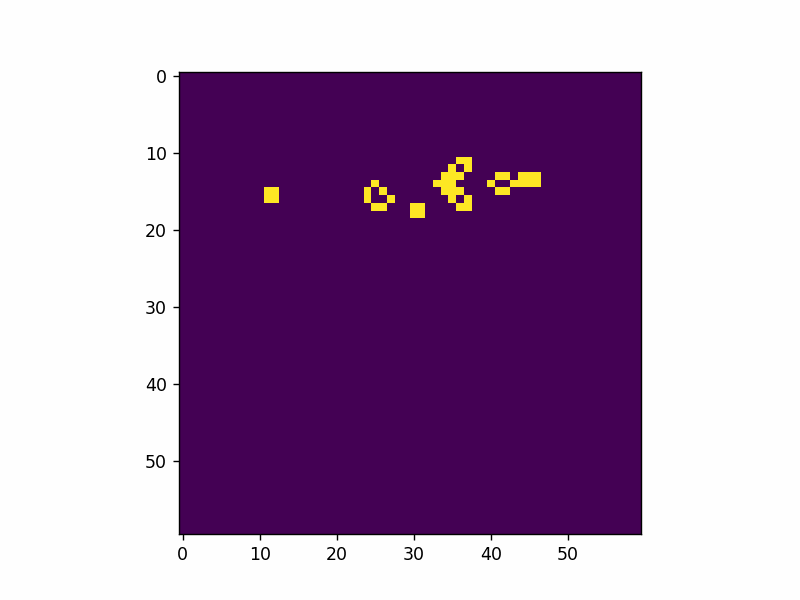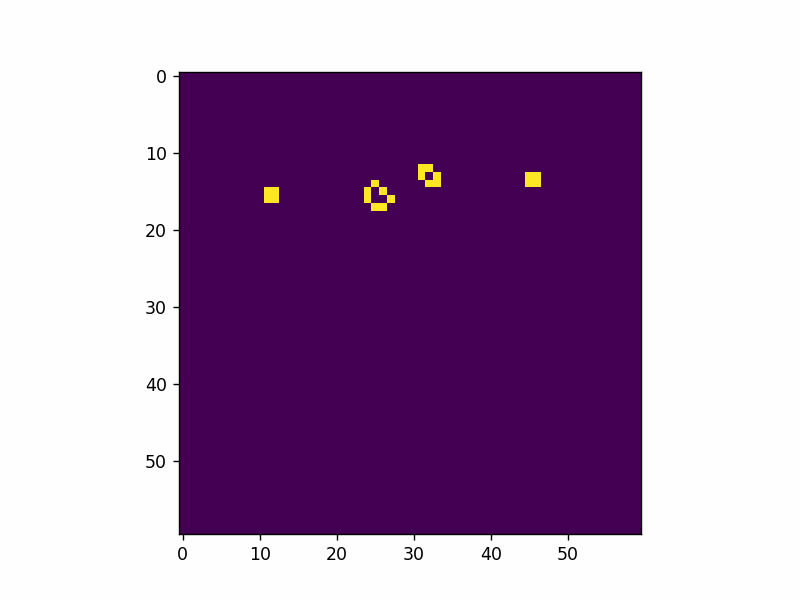
That’s all I have for now. Live long and prosper.
What is the image I clicked on to open this article?
The image is of Ian Malcom from Jurrassic Park delivering his famous line, “Life, uh, finds a way.”